Table of Contents
Preface:
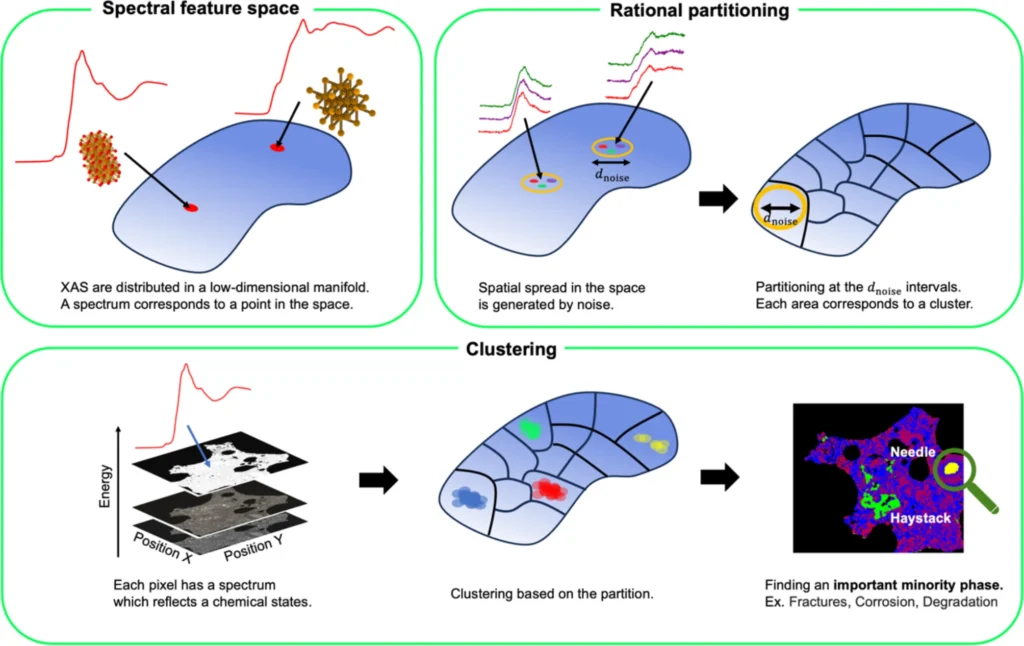
Spectral imaging has revolutionized data processing in numerous fields by acquiring intricate information across diverse wavelengths. Nevertheless, the vast quantities of data produced make the organization and extraction of significant patterns a critical task. An efficient method for managing data complexity is clustering. Clustering aggregates analogous data points, facilitating the discovery of latent structures within the dataset. Nonetheless, the elevated dimensionality and extensive scale of spectral data pose considerable challenges. Logical segmentation of the spectral feature space can provide an effective strategy to address these issues, facilitating more efficient and precise grouping of spectral picture data.
Comprehending Spectral Image Data:
Spectral image data refers to images that contain information from the entire electromagnetic spectrum, extending beyond the visible light range. In contrast to conventional photographs that solely record red, green, and blue wavelengths, spectral images acquire data throughout hundreds or even thousands of wavelengths. Depending on the resolution, we refer to this as hyperspectral or multispectral imaging. These databases are exceptionally comprehensive, providing insights unattainable through conventional photographs. Various domains such as satellite remote sensing, medical diagnostics, environmental monitoring, and agriculture use spectral imaging.
Obstacles in Spectral Data Clustering:
Clustering spatial data is a challenging task. The vast amount of data involved is a significant challenge. Spectral datasets can readily exceed hundreds of gigabytes, rendering conventional grouping algorithms inefficient or impractical. The elevated dimensionality of the data presents an additional issue known as the “curse of dimensionality,” in which an increase in dimensions complicates the ability of clustering algorithms to discern significant groupings. This results in elevated computational expenses and suboptimal clustering efficacy in the absence of meticulous pretreatment.
What constitutes spectral feature space?
Spectral feature space is the multidimensional representation of spectral data, with each dimension representing a certain wavelength or spectral band. The data points in this space represent a variety of materials or things, characterized by their distinct spectral fingerprints. Structuring and grouping these points inside the spectral feature space facilitates the recognition of significant patterns, such as identifying regions of vegetation, water bodies, or urban development in satellite imaging. Efficiently partitioning this feature space is essential for properly managing huge datasets.
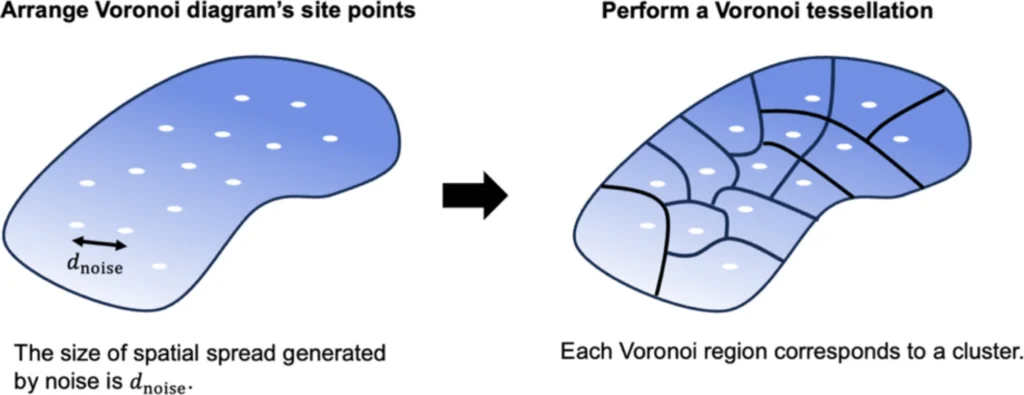
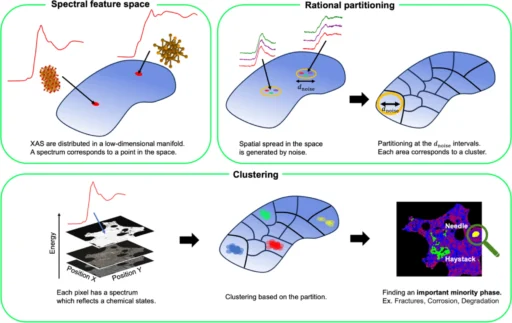
Realizing rational partitioning. By arranging Voronoi diagram site points at intervals of measurement noise and performing Voronoi tessellation, it can be approximately realized to divide the spectral feature space at the interval.
Rational partitioning: definition and significance:
Rational partitioning denotes the systematic division of the spectral feature space into smaller, more manageable portions. This approach is crucial for clustering large datasets since it streamlines the clustering challenge by operating on smaller data groups. By strategically partitioning the feature space, the clustering algorithm can concentrate on pertinent segments of the data, thereby decreasing computational expenses and enhancing clustering precision. Rational partitioning is crucial in situations where the data volume is excessive for single processing or when several parts of the feature space exhibit unique properties.
Methods for Partitioning Spectral Feature Space:
Numerous methodologies exist for dividing spectral feature space, each possessing distinct advantages and disadvantages.
Grid-based partitioning: Segments the feature space into a grid of uniformly sized cells, facilitating management and processing. Nonetheless, it may not consistently correspond with the inherent data distribution.
Random partitioning: Divides the space into arbitrary parts, offering adaptability but possibly resulting in imbalanced partitions.
Adaptive partitioning techniques: These approaches modify partition sizes according to data density, guaranteeing more refined partitions in regions with elevated data concentration.
Machine learning-based partitioning: Machine learning-based partitioning employs methods such as k-means or decision trees to establish data-driven partitions that accurately represent the underlying data structure.
Logical Partitioning Strategy for Clustering:
An effectively devised rational partitioning method considers the configuration of the spectral feature space and the prerequisites of the clustering algorithm. Effective partitioning must minimize the dimensions the algorithm processes while ensuring the partitions encapsulate significant data relationships. In hyperspectral imaging, partitioning may be determined by wavelength zones that correspond to particular materials or chemicals within the image.
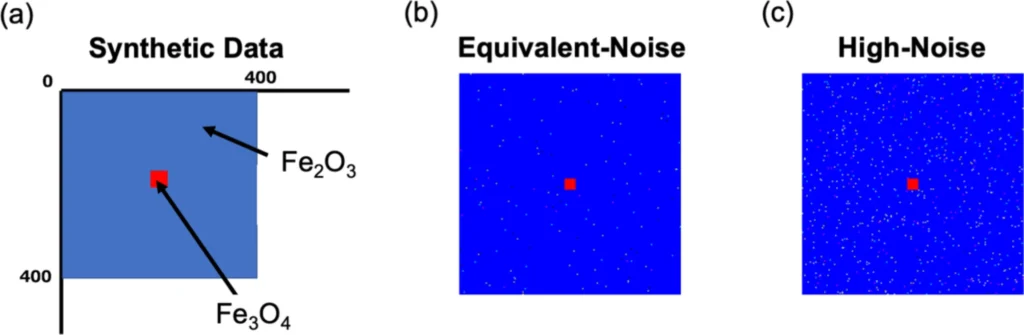
Result of synthetic data analysis. (a) Schematic diagram of the prepared synthetic data. 400 × 400 pixels are filled with Fe2O3 spectrum in all regions except for the central 10 × 10 pixels containing Fe3O4 spectrum. (b) Clustering result by the proposed method where the amount of added noise is equivalent to that used for site points reduction. (c) Clustering results where the amount of noise is high.
Overview of the Spectral Clustering Algorithm:
Spectral clustering algorithms are especially adept at operating within spectral feature spaces. These algorithms utilize the eigenvalues of a similarity matrix obtained from the data to execute dimensionality reduction before clustering. This method is beneficial for high-dimensional data, as it can identify intricate correlations between data points that conventional clustering techniques may overlook.
Managing Extensive Spectral Data:
Efficiency is paramount in the context of extensive spectral datasets. Computational methods like parallel processing and distributed systems can greatly enhance the efficiency of clustering jobs. Furthermore, enhancing data storage and retrieval methods, such as utilizing hierarchical data formats (HDF) or cloud-based solutions, guarantees that even exceedingly huge datasets can be processed without overburdening system resources.
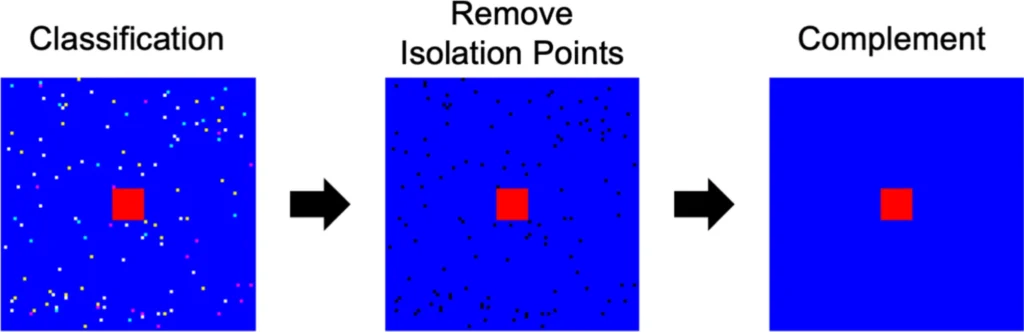
Result of improvement of noise redundancy using spatial correlation. First, remove the isolation points, then complement the points.
Enhancing Clustering with Partitioning:
Dividing the spectral feature space diminishes the computational difficulty of clustering by segmenting the effort into smaller, more manageable components. Determining the appropriate division granularity is essential. Excessively coarse clustering may overlook significant nuances in the data, while excessively fine clustering may render processing costs prohibitive relative to the advantages.
Metrics for evaluating clustering performance:
We can use a variety of performance indicators to evaluate the effectiveness of clustering. These encompass:
Silhouette score: The silhouette score evaluates how similar a point is to its cluster in comparison to other clusters.
Davies-Bouldin Index: Assesses the mean similarity ratio between each cluster and its closest analogous counterpart. Enhancing partitioning can frequently improve these metrics, yielding more precise and significant clustering outcomes.
Utilization of Rational Partitioning across Diverse Domains:
Rational partitioning methodologies have numerous applications.
Remote sensing: Remote sensing facilitates the observation of environmental alterations, urban development, and agricultural vitality.
Medical imaging: Medical imaging can identify tissue problems by analyzing their spectral signatures.
Industrial inspection: Aids in quality control by detecting material faults or contamination in industrial operations.
Comparative Examination of Partitioning Methods:
Diverse partitioning methodologies provide distinct degrees of precision and computational efficacy. Grid-based partitioning is simple to do but lacks flexibility. Adaptive partitioning offers a more sophisticated methodology but necessitates increased processing resources. The appropriate method is selected based on the specific data and clustering objectives. Clustering results of the large-scale measurement data of an actual material and results of SEM-EDX measurements. The colors correspond to clusters representing different chemical states, and the shading shows the component ratios and iron density in the clustering result image. SEM-EDX measurements show that the yellow phase is Mg-rich phase.

Case Study: Clustering in Hyperspectral Imaging
In hyperspectral imaging, reasonable partitioning can significantly enhance clustering results. Partitioning according to specific wavelength zones associated with known materials can facilitate the classification of terrain types, such as differentiating between woods, lakes, and urban areas in satellite imaging.
Final Assessment:
Logical segmentation of the spectral feature space is an essential method for enhancing the efficacy of grouping extensive spectral picture data. Decomposing the data’s complexity facilitates more efficient and precise clustering, resulting in important insights across various industries. As datasets expand in size and complexity, the demand for sophisticated partitioning techniques will escalate, paving the way for novel advancements in spectral data analysis.
Frequently Asked Questions:
1). What is spectral clustering?
Spectral clustering is a technique that employs the eigenvalues of a similarity matrix to diminish data dimensionality and discern clusters.
2). What distinguishes spectral data from conventional image data?
Spectral data encompasses information across numerous wavelengths beyond the visible spectrum, providing more comprehensive insights than standard RGB photos.
3). What is the significance of partitioning when clustering large datasets?
Partitioning divides extensive datasets into smaller segments, enhancing clustering efficiency and diminishing computational complexity.
4). What are the constraints of spectral clustering algorithms?
Spectral clustering can be computationally demanding, and it may not scale effectively with very large datasets without appropriate division.
5). Can different data types use partitioning algorithms?
Indeed, partitioning algorithms apply to any high-dimensional data, encompassing text, audio, and time-series data.
For more chemistry blogs, visit chemistry Master